

Simply select the formula that corresponds to the information you have, input your measurements, and let our calculator do the rest. In conclusion, calculating the area of a triangle can be a tricky task, but with our online triangle area calculator, you'll have the solution at your fingertips. Whether you know the base and height, all three sides, or the sides and an angle, our calculator will provide you with accurate results in no time. With our online triangle area calculator, you can easily find the area of a triangle by selecting the formula you want to use and inputting the required measurements. The first one is the `base and height` formula, which is used when the base and height of the triangle are known.
To calculate the area of a triangle, there are three main formulas that are commonly used. Let's start with a basic definition: A triangle is a polygon with three sides. The tally marks on the sides of the triangle indicate the congruence (or lack. The figure below shows an isosceles triangle example. Since the sides of a triangle correspond to its angles, this means that isosceles triangles also have two angles of equal measure. Equilateral triangle area Triangle area through base and height An isosceles triangle is a triangle that has at least two sides of equal length.Through the radius of the circumscribed circle.Through the radius of the inscribed circle.Through two sides and the angle between them.While finding the area of a triangle can be challenging, our online triangle area calculator makes it quick and simple. The area A is equal to the square root of the semiperimeter s times semiperimeter s minus side a times semiperimeter s minus a times semiperimeter s minus base b.Triangles are a fascinating geometric shape, and understanding their area is important in many fields, such as engineering and construction. You can find the area of an isosceles triangle using the formula: The semiperimeter s is equal to half the perimeter. Given the perimeter, you can find the semiperimeter.
BASE OF ISOSCELES TRIANGLE CALCULATOR PLUS
Thus, the perimeter p is equal to 2 times side a plus base b. You can find the perimeter of an isosceles triangle using the following formula: Given the side lengths of an isosceles triangle, it is possible to solve the perimeter and area using a few simple formulas. The vertex angle β is equal to 180° minus 2 times the base angle α.

Use the following formula to solve the vertex angle:

The base angle α is equal to quantity 180° minus vertex angle β, divided by 2. Use the following formula to solve either of the base angles: Given any angle in an isosceles triangle, it is possible to solve the other angles.
BASE OF ISOSCELES TRIANGLE CALCULATOR HOW TO
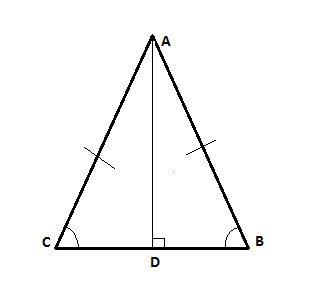
How to Calculate the Angles of an Isosceles Triangle The side length a is equal to the square root of the quantity height h squared plus one-half of base b squared. Use the following formula also derived from the Pythagorean theorem to solve the length of side a: The formula for calculating the area of an isosceles triangle with sides is as follows: Isosceles triangle area (a2 b2 /4) × b where, b the isosceles triangle’s base. The base length b is equal to 2 times the square root of quantity leg a squared minus the height h squared. If the lengths of an isosceles triangle’s equal sides and base are known, the triangle’s height or altitude may be computed. Use the following formula derived from the Pythagorean theorem to solve the length of the base side: Given the height, or altitude, of an isosceles triangle and the length of one of the sides or the base, it’s possible to calculate the length of the other sides. How to Calculate Edge Lengths of an Isosceles Triangle We have a special right triangle calculator to calculate this type of triangle. Note, this means that any reference made to side length a applies to either of the identical side lengths as they are equal, and any reference made to base angle α applies to either of the base angles as they are also identical. When references are made to the angles of a triangle, they are most commonly referring to the interior angles.īecause the side lengths opposite the base angles are of equal length, the base angles are also identical. The two interior angles adjacent to the base are called the base angles, while the interior angle opposite the base is called the vertex angle. The equilateral triangle, for example, is considered a special case of the isosceles triangle. However, sometimes they are referred to as having at least two sides of equal length. Isosceles triangles are typically considered to have exactly two sides of equal length. The third side is often referred to as the base. An isosceles triangle is a triangle that has two sides of equal length.


 0 kommentar(er)
0 kommentar(er)
